3 条件分岐とループ

ここでは，条件分岐とループ（繰り返し（イテレーション））の２つの構文を学びます．条件分岐とループではブロックという概念がキーポイントです．この２つの処理を知るとかなり複雑なプログラムを作ることができます．条件分岐とループの中身に入る前にキーボードからの入力をプログラム内で使えるような入力関数を説明します．

3.1 入力関数（input( )）

以下のようなプログラムを作成してみましょう（it03_01.py）．

In [1]:
# キーボードから入力された名前に"さん"をつけるプログラム(it03_01.py)
print("名前を入力してください\n") # 名前を入力してもらうように誘導
name = input()                    # キーボードからの入力を文字列として受け付ける
print(name + "さん")              # nameに入っている文字列に"さん"を付けたして表示

名前を入力してください

武蔵野
武蔵野さん

１行目で名前を入力してもらうように誘導し、２行目でキーボードからの入力をnameに代入し、３行目で文字列nameに"さん"を付け加えて表示してます．1行目の\nは改行を意味してます．また，input()関数はキーボードからの入力を待つので「Enter」キーを押すまで次の行に進みません． それでは，続いて計算してみましょう．以下のようなプログラムを作成してください.

In [2]:
# キーボードから入力した半径から円の面積を求めるプログラム１
pi = 3.14                         # 円周率の値
print("半径を入力してください\n") # 半径を入力してもらうように誘導
radius = input()                  # キーボードからの入力をradiusに代入
print(radius**2*3.14)             # 半径radiusから円の面積を求めて表示

半径を入力してください

3

---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
<ipython-input-2-2a9aa401b55c> in <module>()
      3 print("半径を入力してください\n") # 半径を入力してもらうように誘導
      4 radius = input()                  # キーボードからの入力をradiusに代入
----> 5 print(radius**2*3.14)             # 半径radiusから円の面積を求めて表示

TypeError: unsupported operand type(s) for ** or pow(): 'str' and 'int'

上述のようにエラーが表示されます．実は，input()はキーボードから入力されたものを文字列として解釈します．文字列変数には**という演算は定義されてませんのでエラーとなった訳です．そこで，入力された文字列を整数に変換する必要があります．

In [2]:
# キーボードから入力した半径から円の面積を求めるプログラム２
pi = 3.14                         # 円周率の値
print("半径を入力してください\n") # 半径を入力してもらうように誘導
radius = input()                  # キーボードからの入力をradiusに代入
radius = int(radius)              # 文字列型"radius"を整数型"radius"へ変換
print(radius**2*3.14)             # 半径radiusから円の面積を求めて表示

半径を入力してください

3
28.26

これで無事計算可能になりました．このように，input()関数はキーボードからの入力をプログラムへ引き渡す事ができ，イロイロ値を変えて計算する場合に便利です．

3.2 条件分岐1 （if else）

それでは，「条件によって処理を振り分ける」文（if else 文）について紹介します．先ほど，作った「キーボードから入力された名前に"さん"をつけるプログラム」（it03_01.py）を変更して，「キーボードから「武蔵野」という名前を入力したら"いいよ♪"を返し，それ以外が入力されたら"…ごめんなさい"」を出力するプログラムを作成します．

In [4]:
# キーボードから入力された名前に応じて出力が変わるプログラム
print("名前を入力してください\n") # 名前を入力してもらうように誘導
name = input()                    # キーボードからの入力を文字列として受け付ける
print(name+"くん　「遊びにいこ」") #会話部分 「name+くん　「遊びにいこ」」が表示される
if name == "武蔵野":              # もし，nameと"武蔵野"が一致したら以下の「ブロック」の処理を行う
    print("Pyちゃん 「いいよ♪」")
else:                             # "name"と"武蔵野"が一致しなければ下記の「ブロック」の処理を行う
    print("Pyちゃん　「…ごめんなさい」")

名前を入力してください

きの
きのくん　「遊びにいこ」
Pyちゃん　「…ごめんなさい」

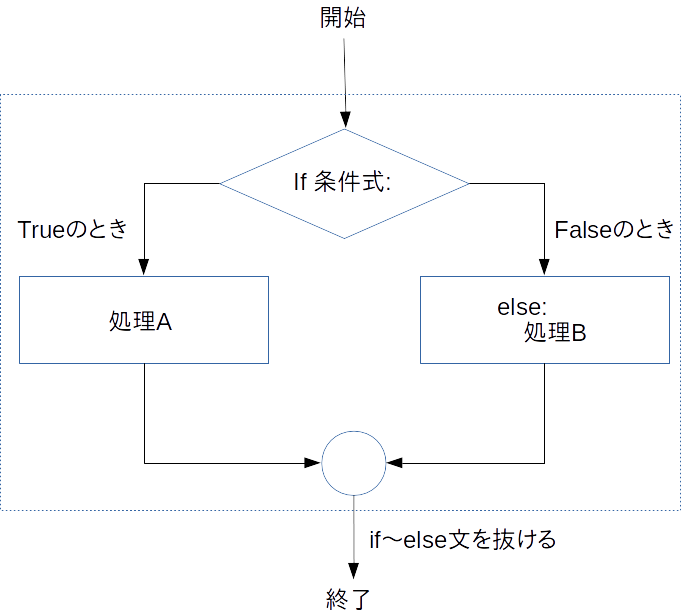
「条件分岐」、「繰り返し（この後でやる）」の文で重要なのはブロックという考え方です． 具体的に上のプログラムを読みながら考えます．このプログラムの重要部分は5行目以降であり，5行目と6行目で1つの処理が行われています．5行目は「if name == "武蔵野":」は「もし，nameと"武蔵野"が等しかったら次の処理をしなさい」という条件文になってます。 ifで始まり:で終わります．そして，6行目では4文字分スペースで空いています（tabキーで4文字分スペースが空きます）．これをインデントと呼びPythonではとても重要な意味を持っております．今回のプログラムの場合「5行目の条件を満たす場合，6行目のみが実行されます．if文の次の行（複数行の場合もある）のインデントがそろった部分を「（コード）ブロック」と呼びます．（実は他の多くの言語ではブロックを表すのに括弧（{}など）を使用します．括弧を使うとプログラムの書き方が自由になり過ぎ，他の人が読みにくくなることが知られています．）

if 条件:

    文１
    文２
    ・・・

else:

    文３
    文４
    ・・・

文１，文２のようにインデントがそろっている部分をまとめて「ブロック」と呼び，同様に文３と文４もまとめて「ブロック」と呼びます．ifの「条件」を満たしている場合「文１，文２のブロック」が実行され，条件を満たさない場合「文３，文４のブロック」が実行されるわけです．条件部分では「何らかの比較」が為されるので，そこで使われる演算子を比較演算子と呼びます．良く使われる比較演算子には次のようなものがあります．

比較演算子

演算子 説明
`x == y` `x`と`y`が等しい場合にTRUE（真）となります．代入（`=`）と違うので注意してください．
`x != y` `x`と`y`が等しくない場合にTRUE（真）となります．
`x < y,` `x > y` `x`と`y`の大きさを比較します．「`>`」は左側が大きい場合にTRUE（真）となり，「<」は右側が大きい場合にTRUE（真）となります．`x`と`y`が等しい場合はFALSE（偽）となります．「`x < y < z`」のように複数の不等号を組み合わせて書くこともできます．
`x <= y,` `x >= y` xとyが等しい場合も含み，大きさを比較します．不等号の位置はイコールの左側になります．「x<=y<=z」のように複数の不等号を組み合わせて書くこともできます．
`x in y` シーケンス（文字列やリストなど）に，ある要素などが含まれるかどうかを比較します．xという要素がyの中に含まれる場合にTRUE（真）となります．
In [1]:
# 入力された整数を偶数・奇数に分類するプログラム　(it03_02.py)
print("整数を入力してください")
any_int = int(input())                # 整数を自由に入力
if any_int % 2 == 0:                  # any_intが2で割り切れるか否か判断(条件1)
    print("入力された整数は偶数です")
else:                                 # 条件1に当てはまらないときに下記のブロックを実行
    print("入力された整数は奇数です")
print("計算終了")

整数を入力してください
3
入力された整数は奇数です
計算終了

基本問題1

it03_02.pyのif文の条件を「any_int % 2 != 0」とした時に，同じ結果を出力するようにプログラムを変更しなさい．

3.3 条件分岐２　（if-elif文）

条件分岐の2番目のパターンです．最初に調べた条件が成り立たなかったとき，さらに別の条件を調べたい場合，if-elif．下記のプログラムは入力された3つの整数（x, y, z）の中で最も小さいものを出力するプログラムです．

In [10]:
# 入力された3つの整数のうち最小値を求めるプログラム１　(it03_03.py)
print("整数を3つ入力してください")
print("整数1")
x = int(input())               # xに整数1を代入
print("整数2")
y = int(input())         　　　# yに整数2を代入
print("整数3")
z = int(input())               # zに整数3を代入

if x < y and x < z:            # x < y かつ　x <  zを満たす場合下のブロックを実行 （条件１）
    print("整数1が最も小さい")
elif y < z:                    # (条件1を満たさず，かつ ) y < zを満たす場合に下のブロックを実行（条件2）
    print("整数2が最も小さい")
else:                          # 条件1,2を満たさない場合
    print("整数3が最も小さい")

整数を3つ入力してください
整数1
5
整数2
100
整数3
-1
整数3が最も小さい

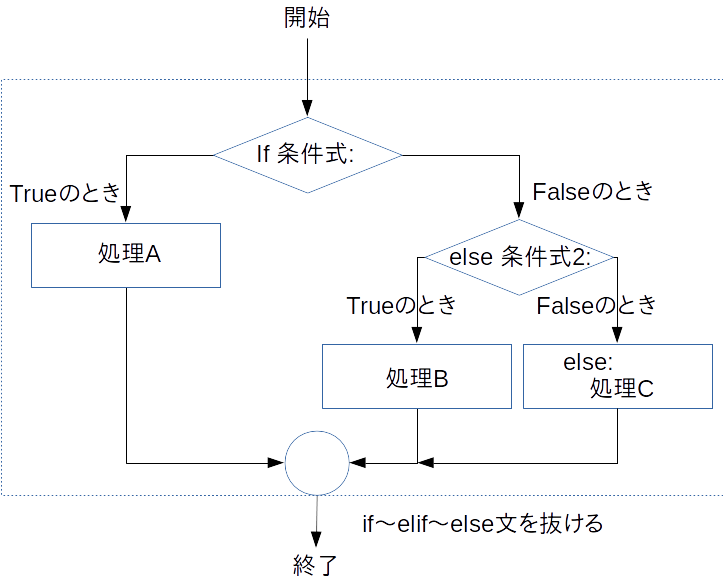
１，「if x < y and x < z:」の条件式は 「x < y かつ　x < z」であるときに下のブロック「print("整数1が最も小さい")」が実行されます（"and"については後で説明します）． ２，その条件に当てはまらない場合その下の「elif y < z:」の条件が比較され当てはまる場合下のブロック 「print("整数2が最も小さい")」が実行されます． ３，１と２のどちらの条件にも当てはまらない場合，下のブロック「print("整数3が最も小さい")」が実行されます．

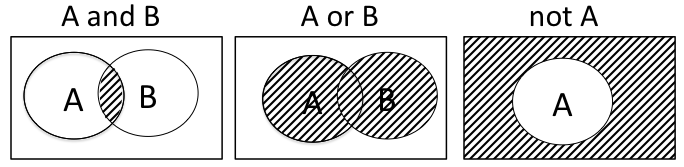
ところで，１行目に"and"という演算子が使われてます．「式１ and 式２」という形で使われ，「式１　かつ　式２」という条件を表しています．このような演算子を論理演算子と言います．

論理演算子

論理演算子 説明
A and B 条件Aと条件B両方を満たす場合にTRUE（真）となります．
A or B 条件Aあるいは条件B，もしくはその両方を満たす場合にTRUE（真）となります．
not A 条件Aを満たす場合にFALSE（偽）となります．

3.4 条件分岐３　（ネスト）

上のプログラムit03_03.pyはネスト（入れ子構造の事）と言われる他の方法でも書く事ができます．

In [1]:
# 入力された3つの整数のうち最小値を求めるプログラム２　(it03_04.py)
print("整数を3つ入力してください")
print("整数1")
x = int(input())               # xに整数1を代入
print("整数2")
y = int(input())               # yに整数2を代入
print("整数3")
z = int(input())               # zに整数3を代入

if x < y and x < z:            # x < y かつ　x <  zを満たす場合下のブロックを実行 （条件１）
    print("整数1が最も小さい")
else:
    if y < z:                  # (条件1を満たさず，かつ ) y < zを満たす場合に下のブロックを実行（条件2）
        print("整数2が最も小さい")
    else:                          # 条件1,2を満たさない場合
        print("整数3が最も小さい")

整数を3つ入力してください
整数1
1
整数2
-2
整数3
-3
整数3が最も小さい

実際プログラムを書く時にはネストよりも"if elif"文を用いて書いた方が複雑にならずにすみます．

レポート課題3

入力された実数の絶対値を表示するプログラムを作成して下さい．it03_学籍番号.ipynbとしてメールで提出しなさい． 〆切：10/16(月）

応用問題

２次方程式$ax^2+bx+c=0$の実数解を求めるプログラムをヒントにある条件を考慮して作成してください．なお，平方根はスクリプトファイルの1行目に「import math」というおまじないを書き，「a」という変数の平方根が欲しい場合は「math.sqrt(a)」として下さい．

ヒント１

解の公式より，判別式を$D=b^2 -4ac$とし以下のパターンに場合分けします．

  1. 係数$a, b$がともに$0$ならば解は存在しない．

  2. 係数$a$が$0$であり，係数$b$が$0$でなければ1次式であり解は1つ．

  3. 係数$a$が$0$でなく，判別式$D$が$0$より大きければ2つの実数解．

  4. 係数$a$が$0$でなく，判別式$D$が$0$であれば重解．

  5. 係数$a$が$0$でなく，判別式$D$が$0$より小さければ実数解なし（虚数解）．

【出力例】
ax^2 + bx + c = 0 の係数a, b, cを入力してください aは？ 1 bは？ 4 cは？ 3 解は2つあり，x1= -1.0 , x2= -3.0

以下は大ヒントになります。「自分で考えよう」書かれてある部分を適切に書けば正解コードとなります．
【ヒント】

import math

print("ax^2 + bx + c = 0 の係数a, b, cを入力してください")
print("aは？")
a = int(input())
print("bは？")
b = int(input())
print("cは？")
c = int(input())

if 「自分で考えよう」:
    if 「自分で考えよう」:
        print("係数がおかしい")
    else:
        x = -c / b
        print("解は%d" % x )
else:
    D = 「自分で考えよう」
    if 「自分で考えよう」:
        x1 = (-b + math.sqrt(D)) / (2 * a)
        x2 = (-b - math.sqrt(D)) / (2 * a)
        print("解は2つあり，x1=",  x1, ", x2=", x2)
    elif 「自分で考えよう」:
        x = (-b)/2
        print("解は重解となり，x=", x)
    else:
        print("解は虚数解となり，実数解は存在しない")

3.5 ループ１（for）

プログラムでは同じ処理を繰り返し処理したい場合があり，そのような処理をループ（繰り返し処理）と言います．Pythonではfor文，while文の２つのループ処理があります．まずはforの使い方について見てみましょう． プログラムでは，$10$回，$100$回というように回数を指定してループを実行するという処理をよく行います．人間では嫌になるような$10^6$回といったループも難なく実行してくれます．早速forの使い方を見ましょう．

for文もif文と同様にインデントがそろった部分をブロックと呼びrange()を用い繰り返し回数を表し，ブロック部分が処理されます．繰り返し回数が決まっている場合にはfor文をよく使います．

for 変数 in 繰り返し回数:

    文１
    文２
In [2]:
# forループの動作１ it03_05.py
for item in range(0, 10, 1): # 0から1つずつ9まで順番にitemに代入する
    print(item)

0
1
2
3
4
5
6
7
8
9

for文を使うときは，よくrange()関数を使います．

range([開始], 終了, [ステップ])

[開始]と[ステップ]は省略できます． このプログラムでは2行目にfor文と繰り返し回数が記述されており，3行目で「item」を出力してます．

In [3]:
# forループの動作２(it03_05.pyと同じ動作をする)
for item in range(10): # 0から1つずつ9まで順番にitemに代入する
    print(item)

0
1
2
3
4
5
6
7
8
9

ステップ数を変更することで，2つ置きに代入することもできます．

In [4]:
# forループの動作３(2つ置きに代入する)　it03_06.py
for item in range(0, 10, 2): # 0から1つずつ9まで順番にitemに代入する
    print(item)

0
2
4
6
8

基本問題2

先週の1.4で学んだ正３角形を作成するプログラムをforループを用いて簡単にしてください．

3.6 ループ２（while）

ある一定の条件を満たしている間繰り返しを続けたい場合があります．その場合にはwhile文を使います．

while 条件1:

    文1
    文2

whileの後ろ「条件１」が成り立つ限りブロック部分（文１，文２）を繰り返し処理することになります．早速，実際のプログラムを見てみましょう．

In [5]:
# whileループの動作１ 1～10までの和を計算するプログラム it03_07.py
count = 1          # カウンタ変数の初期化
sum=0              # 和を代入する変数の初期化
while count <= 10: # countが10以下の時に下のブロックを実行する
    sum += count   # sum = sum + count と同じ意味
    print("count=", count, "sum=", sum)    # print("count=%d sum=%d" % (count, sum))
    count += 1     # カウンタ変数を１増やす．（つまり，繰り返し回数を数えている）

count= 1 sum= 1
count= 2 sum= 3
count= 3 sum= 6
count= 4 sum= 10
count= 5 sum= 15
count= 6 sum= 21
count= 7 sum= 28
count= 8 sum= 36
count= 9 sum= 45
count= 10 sum= 55

while文ではよく繰り返し回数を数えるカウンタ変数が用いられます．上のプログラムでは「count」がカウンタ変数です．2行目で「count」の初期化を行ってます．3行目では和を代入する変数「sum」を初期化してます．多くのプログラムでは条件分岐や繰り返し処理の前に，このような変数の初期化を行う必要 が出てきます．4行目にwhile文とその条件が記述されてます．5行目で和が計算されてます．6行目で「カウンタ変数の値」と「和の変数の値」を表示してます．7行目でカウンタ変数の値を1増やしてます． プログラムの動きが分かりにくい場合，紙と鉛筆をつかって自分の手でプログラムの計算を手計算してみるのがとても良い方法です（古風と感じるかもしれませんが）．自分の思った計算結果が得られない場合，紙と鉛筆を用いて計算するようにしてください．

while文を用いて無限に処理を繰り返すことが出来ます．2行目と3行目の"#"を取りのぞき実行すると，計算を永遠に続けることとなるので気を付けてください．無限ループの実行を取り消すには[Ctrl]+c です．

In [6]:
#while文による無限ループプログラム it03_11.py
#while True:  whileの条件文が「True」もしくは「1」の時，ブロック部分を無限にくり返す
#    print("無限ループ")

3.7 多重ループ（ネスト）

for, whileのようなループ文はネストすることでループ1の中にループ2があるような多重ループを作ることができます．実行する前にどのように表示されそうか予想してください(プログラムを実行するときは2～4行目の#を外すこと)．

In [7]:
# for文を用いた多重ループ１ it03_09.py
# for count1 in range(3): # 
#    for count2 in range(5):
#        print("count1=", count1, " count2=", count2)

外側のループ（カウンタ変数count1）が1回実行されると，内側のループが続けて5回実行されることが分かります．また，外側のループのカウンタ変数が1増えるたびに内側のループのカウンタ変数が0にリセットされることにも注意してください． 多重ループは数値シミュレーションを実行するときによく出てきますが，2重3重・・・と増やすにつれ計算回数が著しく増大します（数学の言葉では「指数関数的に増大する」といいます）．このような計算回数を減らす計算方法（アルゴリズム）を見つけることはとても重要な仕事です．

計算回数 $N$ $10$ $100$ $100000$ $1000000$
$\log N$ およそ$3$ $6$ $16$ $19$
$N \log N$ $30$ $600$ $1,600,000$ $19,000,000$
$N^2$ $100$ $10,000$ $10,000,000,000$ $1,000,000,000,000$

3.8 break文とcontinue文

ループを実行するときにある条件を満たしたらループを途中で終了したい場合がありそのようなときにbreak文を使います．break文の後のブロックは実行せずループを抜け出します．また，continue文はcontinue文の後ろのブロックは実行せずループの初めに処理を戻します．

In [8]:
# break文を用いて50回で無限ループを抜け出すプログラム it03_10.py
count = 0
while True:
    count +=1
    if( count > 50):
        print("count=", count)
        break

count= 51
In [12]:
# 敢えてcontinue文を用いて1～20までの中から偶数のみを表示させるプログラム　it03_11.py
for i in range(1, 20):
    if ((i % 2) == 1):
        continue
    print(i)

2
4
6
8
10
12
14
16
18

レポート課題4

pythonでは正の数の２乗はx**2で計算できますが，敢えて足し算とループ文を用いて入力した変数の２乗を出力するプログラムを作ってください．「it04_学籍番号.ipynb」としてメールで提出しなさい． 〆切：10/30(月)

【出力例】

自由に整数を入力してください？
5
5 の2乗は 25

応用問題2

次のプログラムは「総当たり法」を用いて，与えられた整数$x$に対して「整数で表現できる立方根」を求めるプログラムです（整数で表現できる立方根がある場合（例. $2^3=8$）とない場合（例. $7$）で表示を変更してます）．「総当たり法」とは$0$から順番に全ての数について条件に当てはまるか否か調べる方法の事です．下記のプログラムを穴埋めし完成させなさい．（abs(x)はxの絶対値を返す関数です）

【出力例】

任意の整数を入力してください？-8
-8 の完全立方は -2

【ヒント】与えられた整数xに対して「整数で表現できる立方根」を求めるプログラム（総当たり法it03_12.py

x = int(input("任意の整数を入力してください？"))
for cube_root in range(「自分で考えよう」): # 0から与えた整数の絶対値までくり返すループ
    if cube_root**3 >= abs(x): # 0から与えられた整数xの絶対値まで順にカウンタ変数cube_rootを３乗し，xの絶対値以上の場合ループを抜ける
        break
if 「自分で考える」: # ループを抜けたときにおいて，cube_rootの３乗がxの絶対値の３乗に等しくない場合
    print(x, "は完全立方ではありません．")
else:                      # ループを抜けたときにおいて，cube_rootの３乗がxの３乗に等しい場合
    if x < 0:              # xが負の場合
        「自分で考える」 #cube_rootを負にする
    print(x, "の完全立方は", cube_root)

応用問題3

次のプログラムは，またもや「総当たり法」を用いて平方根のおおよその値（近似値）を求めるプログラムです．実際の答えからある一定の範囲内（epsilon）にある答えを十分に近いものとして近似値を計算します． $x=25$と $x=123456$について計算して出力の違いを確認して下さい．

【出力例】

0.0 12345
repCount = 1234500
12345 の平方根（近似値）を作れませんでした

【ヒント】与えられた整数の平方根を近似的に求めるプログラム（総当たり法）it03_13.py

x = 12345 # 与える整数
epsilon = 0.1 # ほぼ同じ値とみなす範囲
step = epsilon**2 # 刻み幅の設定
repCount = 0
ans = 0.0 # 近似的な平方根を表す数
print(ans, x)
while 「自分で考えよう」: # stepの刻み幅で大きくなる数ansの２乗と与えた整数の差の絶対値がepsilonの範囲以上，かつansが与えた整数以下という条件
    ans += step  # stepの刻み幅だけ大きくする
    repCount+= 1 # カウンタ変数を1増やす
    #print(ans)
print("repCount =", repCount) # 繰り返し回数の表示
if 「自分で考えよう」: # ansの２乗と与えた整数の差の絶対値がepsilonの範囲以上という条件
    print(x, "の平方根（近似値）を作れませんでした．")
else:                          # ansの２乗と与えた整数の差の絶対値がepsilonの範囲以上という条件
    print(ans, "は", x, "の平方根にとても近いです．")

$x=25$の場合には平方根の近似値をepsilonの範囲内で求めることに成功しますが，$x=12345$の場合には平方根の近似値を求めることに失敗してます． 上述の結果はステップサイズ（step）が大きすぎepsilonの範囲内で近似値を見つけることが出来なかった事が原因となってます．